How To Draw Angular Wave Functions

Electronic Angular Wavefunction

1. Final updated

2. Save as PDF

Page ID

2524

The electronic angular wavefunction is one spatial component of the electronic Schrödinger wave equation, which describes the motion of an electron. It depends on athwart variables, \(\theta\) and \(\phi\), and describes the direction of the orbital that the electron may occupy. Some of its solutions are equal in energy and are therefore called degenerate.

Introduction

Electrons tin exist described as a particle or a wave. Because they exhibit wave behavior, in that location is a wavefunction that is a solution to the Schrödinger wave equation:

\[\lid{H}\Psi(r,\phi,\theta,t)=E\Psi(r,\phi,\theta,t)\]

This equation has eigenvalues, \(East\), which are energy values that correspond to the different wavefunctions.

Spherical Coordinates

To solve the Shrödinger equation, spherical coordinates are used. Spherical coordinates are in terms of a radius \(r\), equally well as angles \(\phi\), which is measured from the positive x centrality in the xy plane and may be between 0 and \(2\pi\), and \(\theta\), which is measured from the positive z axis towards the xy plane and may be betwixt 0 and \(\pi\).

Figure 1: Spherical Coordinates

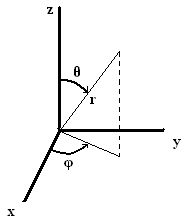
\(10=rsin(\theta)cos(\phi)\)

\(y=rsin(\theta)sin(\phi)\)

\(z=rcos(\theta)\)

Electronic Wavefunction

The electronic wavefunction, \(\Psi(r,\phi ,\theta ,t)\), describes the wave behavior of an electron. Its value is purely mathematical and has no corresponding measurable concrete quantity. However, the foursquare modulus of the wavefunction, \(\mid \Psi(r,\phi ,\theta ,t)\mid ^2\) gives the probability of locating the electron at a given set of values. To employ separation of variables, the wavefunction can be expressed as

\(\Psi(r,\phi, \theta ,t)=R(r)Y_{fifty}^{m}(\phi, \theta)\)

\(R(r)\) is the radial wavefunction and \(Y_{fifty}^{m}(\phi, \theta)\) is the angular wavefunction. Separating the angular variables in \(Y_{l}^{yard}(\phi, \theta)\) gives

\(Y_{l}^{m}(\phi, \theta)=\left[\dfrac{2l+1}{4\pi}\left(\dfrac{(l-\mid m \mid)!}{(l+\mid m \mid)!}\right)\correct]^{\frac{one}{2}}P_l^{\mid chiliad \mid}(cos(\theta))eastward^{im\phi}\)

where \(P_l^{\mid one thousand \mid}(cos(\theta))\) is a Legendre polynomial and is only in terms of the variable \(\theta\). The exponential function, which is but in terms of \(\phi\), determines the phase of the orbital.

For the angular wavefunction, the foursquare modulus gives the probability of finding the electron at a point in infinite on a ray described by \((\phi, \theta)\). The angular wavefunction describes the spherical harmonics of the electron'southward motion. Because orbitals are a cloud of the probability density of the electron, the foursquare modulus of the angular wavefunction influences the direction and shape of the orbital.

Quantum Numbers and Orbitals

In that location are 3 quantum numbers defined by the Schrodinger wave equation. They are \(n\), \(l\), and \(m_{l}\). Each combination of these breakthrough numbers depict an orbital. Values for \(northward\) come up from from the radial wavefunction. \(n\) may be ane, 2, 3... Because they evolved from the separation of variables performed to solve the wavefunction, solutions to the angular wavefunction are quantized by the values for \(l\) and \(m_{l}\). Acceptable values for \(l\) are given by \(50=n-one\). The corresponding values for \(m_{l}\) are integers between \(-l\) and \(+l\).

Degeneracy and p, d and f Orbitals

Orbitals descrbed by the same \(n\) and \(l\) values but different \(m_{fifty}\) values are degenerate, meaning that they are equal in energy but vary in their direction and, sometimes, shape. For \(p\) orbitals, \(l=ane\), giving iii \(m_{l}\) values and thus, 3 degenerate states. They are \(p_{ten}\), \(p_{y}\)and \(p_{z}\). \(d\) orbitals have \(50=2\), giving v degenerate states. These are \(d_{xy}\), \(d_{xz}\), \(d_{yz}\), \(d_{z^2}\), \(d_{x^ii-y^2}\). \(f\) orbitals accept \(l=3\), giving a total of seven degenerate states.

References

1. McMahon, David. (2006) Quantum Mechanics Demystified New York: McGraw-Hill.
2. McGervey, J. D. (1995) Breakthrough Mechanics: concepts and applications San Diego:Academic Press.

Problems

i. Which quantum numbers depend on the angular wavefunction?

2. Give the quantum numbers defined by the athwart wavefunction for a \(d_{z^two}\) orbital.

3. Given that the spherical representation of the \(d_{x^2-y^2}\) orbital is \(r^2 sin^{ii}(\theta) cos(2\phi)\), bear witness that this matches the characterization for the orbital, \(x^2-y^ii\). Hint: \(cos(2x)=cos^2(x)-sin^2(x)\)

Solutions:

1. \(l\) and \(m_{fifty}\)

2. \(l=2\) and \(m_{50}=two,1,0,-i,-2\)

3. \(r^2 sin^{2}(\theta)cos(2\phi)=r^2 sin^{2}(\theta)(cos^2(\phi)-sin^two(\phi))\)

\(r^ii sin^{2}(\theta)cos^ii(\phi)-r^2 sin^{2}(\theta)sin^2(\phi)\)

Since \(x=rsin(\theta)cos(\phi)\) and \(y=rsin(\theta)sin(\phi)\),

\(r^two sin^{ii}(\theta) cos(2\phi)=x^2-y^2\)

Contributors and Attributions

• Bryn Ellison

Source: https://chem.libretexts.org/Bookshelves/Physical_and_Theoretical_Chemistry_Textbook_Maps/Supplemental_Modules_(Physical_and_Theoretical_Chemistry)/Quantum_Mechanics/10%3A_Multi-electron_Atoms/Electronic_Angular_Wavefunction

Posted by: murphyussighboult1999.blogspot.com

Share this post